-
Notifications
You must be signed in to change notification settings - Fork 416
[PROP] Series evolution
This here is a sketch of a future of the series-related part of Red. Fill it in as you wish.
The place for discussion is here: https://github.com/red/REP/issues/54
What can we achieve by pursuing this undertaking?
- A strict definition of each series-related function (SRF) in a common model, that gives us:
1.1. An overview of the series situation, as a whole, that will become:
1.1.1. A learning material, where one could see how things work in general.
1.1.2. A foothold for further SRF refinement. Brain can only hold so much data in it's cache, and a convenient overlook of the model can lead to more improvements.
1.2. A possibility to write an alternate, high level, implementation of all SRFs, that gives us:
1.2.1. Means to test, when uncertain, every SRF against it's high level equivalent.
1.2.2. We could write an automatic test generation system that would do tests for all SRFs with all refinement combinations and all edge cases (almost impossible to cover it all by hand).
1.3. A basis on which spinoffs and alternate implementations of Red can be founded, and to which they should strive to conform.
2. Refinement combination compatibility matrices (RCCMs) for each SRF, which will:
2.1. Serve as a reference material and a hub of ideas behind every SRF implementation detail.
2.2. Bring about all the current quirks and oversights, and may show us new uses for some combinations.
3. Refinement meaning consistency enforcement, by finding and giving the outliers more appropriate names:
3.1. This should enhance readability and improve language learning curve.
Note: the model only concerns series, and no other datatypes.
Let's say throughout the whole period of time Red program runs, we have M unique series in it. Each series has a head position and an associated buffer. We have K ≤ M unique buffers. Buffers are mutable: an operation on one series affects further operations on another series if they share a buffer. To reflect this mutability, we may describe a state machine: a state transition occurs when one of the buffers gets modified.
We have:
- M unique series, M is a nonnegative integer: M∊Nₒ
- K unique buffers, K is a nonnegative integer: K∊Nₒ
Because each series is associated with exactly one buffer, but each buffer can be associated with zero or more series, we have K≤M
A buffer B is an (infinite for simplicity!) sequence of values, defined on the integer set Z.
It maps an integer into a value: ∀i∊Z: B(i)∊V, where V is a set of all values that Red can possibly represent
Each series is associated with an index - an integer, which we will call "offset": Oₘ∊Z, 1≤m≤M
Each buffer is associated with length, or tail - a nonnegative integer: Nₖ∊Nₒ, 1≤k≤K
A buffer is called "empty" if it's associated length equals zero.
A timeline, from the program startup, up to it's current state, can be represented by a nonnegative integer instruction number t: t∊Nₒ.
State Aₜ of the program at time t≥0 consists of:
- K buffers: Bₖₜ(i), 1≤k≤K, Bₖₜ(i) is a function of integer
- K lengths: Nₖₜ, 1≤k≤K - size of usable data in k-th buffer Bₖ
- M buffer numbers: Kₘₜ, 1≤m≤M - associates k-th buffer Bₖ to m-th series Sₘ
- M offsets: Oₘₜ, 1≤m≤M
An instruction represents the transition of state Aₜ into next state Aₜ₊₁, during which only one of (Bₖₜ,Nₖₜ,Kₘₜ,Oₘₜ) can be changed.
The whole timeline A is a matrix of 4 columns: Bₖₜ(i),Nₖₜ,Kₘₜ,Oₘₜ, and T rows, where T is the count of instructions a program performs before termination.
At the time t=0:
- all buffers are "empty", meaning their lengths are set to zero: Nₖₒ = 0, 1≤k≤K
- all series are "at their head", meaning their offsets are set to zero: Oₘₒ = 0, 1≤m≤M
Series-to-buffer associations are currently constant: Kₘₜ = Kₘₒ
For simplicity, each buffer and series always exist, they are never created or destroyed. Unused and not yet declared series/buffers are simply considered not being accessed.
When we need to "create" a new (temporary) m₁-th series, with a new k₁-th buffer, we just represent it as a magical choice of a series that isn't used anywhere else in the program and which buffer is not shared with any other series (∀m≠m₁: Kₘₜ≠k₁). Since we impose no upper limit on M, we're free to do so.
There are only three elementary state transitions through which all other modifying operations (save for random - it's nondeterministic) can be expressed:
-
[rem m j]removes j-th item from m-th series (affecting the buffer and all series that share it) by defining a buffer function Bₖₜ₊₁(i) and buffer length Nₖₜ₊₁ through the previous ones Bₖₜ(i) & Nₖₜ:
let k = Kₘₜ
Bₖₜ₊₁(i) =
Bₖₜ(i), if i < j
Bₖₜ(i+1), if i ≥ j
Nₖₜ₊₁ = Nₖₜ - 1
Instruction is constrained: 0≤j<Nₖₜ (otherwise is an error).
j is an absolute zero-based index, independent of offset Oₘₜ.
-
[ins m j x]inserts item x into m-th series (affecting the buffer and all series that share it) by defining a buffer function Bₖₜ₊₁(i) and buffer length Nₖₜ₊₁ through the previous ones Bₖₜ(i) & Nₖₜ:
let k = Kₘₜ
Bₖₜ₊₁(i) =
Bₖₜ(i), if i < j
Bₖₜ(i-1), if i > j
x, if i = j
Nₖₜ₊₁ = Nₖₜ + 1
Instruction is constrained: 0≤j≤Nₖₜ (otherwise is an error).
j is an absolute zero-based index, independent of offset Oₘₜ.
-
[ofs m j]shifts the offset of m-th series by j:
Oₘₜ₊₁ = Oₘₜ + j
Read-only operations do not involve a state transition and are all done at the same time t.
Some specialty stuff (like reduce - it is not just about tossing items around) may require widening the basis.
These require definition through basic set of state transitions and access to (Bₖₜ(i),Nₖₜ,Kₘₜ,Oₘₜ) state.
Note: equality sign = henceforth is used as "identical" or "defined as", close to Red's =? (same?)
These do not change state.
Let's use () notation for them.
(index? m) =
Oₘₜ + 1 ;) 1-based
(pick m j) =
Bₖₜ(j+Oₘₜ-1), if (j > 0) and (1 ≤ j+Oₘₜ ≤ Nₖₜ)
Bₖₜ(j+Oₘₜ), if (j < 0) and (1 ≤ j+Oₘₜ ≤ Nₖₜ)
none otherwise (including j = 0)
where
k = Kₘₜ
none is a special value (none ∊ V)
(head m) =
m₁ ;) another series
where
Kₘ₁ₜ = Kₘₜ, ;) of same buffer
Oₘ₁ₜ = 0 ;) and zero offset
(tail m) =
m₁ ;) another series
where
Kₘ₁ₜ = Kₘₜ, ;) of same buffer
Oₘ₁ₜ = Nₖₜ ;) and offset equal to tail
(skip m j) =
m₁ ;) another series
where
Kₘ₁ₜ = Kₘₜ, ;) of same buffer
Oₘ₁ₜ = j+Oₘₜ ;) and offset shifted by j
(copy m) =
m₁ ;) another series
where
Kₘ₁ₜ = k₁, ;) of another buffer
k₁ ≠ Kₘₜ ∀m≠m₁, ;) that is unique
Oₘ₁ₜ = 0 ;) offset set to zero
Bₖ₁ₜ(i) = Bₖₜ(i+Oₘₜ) ;) contains identical data
(find m x) =
(find* m x Oₘₜ)
where
(find* m x o) = ;) helper func
none, if o ≥ Nₖₜ
m₁, if Bₖₜ(o) = x
(find* m x o+1), otherwise
where
k = Kₘₜ,
Kₘ₁ₜ = k, ;) new series of same buffer
Oₘ₁ₜ = o ;) at a new offset
The definition of skip above is applicable to free index model only (see below).
What we currently have is (see https://gitter.im/red/red?at=5da8508ef88b526fb95455ef):
(skip m j) =
m₁
where
Kₘ₁ₜ = Kₘₜ,
Oₘ₁ₜ =
j+Oₘₜ, if 0 ≤ j+Oₘₜ ≤ Nₖₜ
0, if j+Oₘₜ < 0
Nₖₜ, if j+Oₘₜ > Nₖₜ
And so on... for all independent refinements and their interdependent combinations...
These do change state.
Let's use [] notation for them.
[clear m] =
m, if Oₘₜ ≥ Nₖₜ
[clear* m]
where
k = Kₘₜ,
[clear* m]:
[rem m Oₘₜ]
= [clear m]
An advanced example PoC:
[change m₁ m₂] =
m₁, if O₂ₜ ≥ Nₖ₂ₜ ;) nothing in m₂
[change* m₁ m₂ O₂ₜ]
where
k₁ = Kₘ₁ₜ,
k₂ = Kₘ₂ₜ,
k₂ ≠ k₁, ;) simplified version - will only work properly on different buffers
[change* m₁ m₂ o]: ;) helper func
[ins m₁ O₁ₜ Bₖ₂ₜ(o)], if (0 ≤ O₁ₜ ≤ Nₖ₁ₜ) and (0 ≤ o)
[rem m₁ O₁ₜ+1], if (0 < O₁ₜ+1 < Nₖ₁ₜ) and (0 ≤ o)
[ofs m₁ 1],
[change* m₁ m₂ o+1], if o < Nₖ₂ₜ ;) until we reach m₂ tail
= m₁ ;) return m₁ after the last changed value
Note that the above change is defined even for negative offsets, it just does not perform a char substitution if Bₖ₂ₜ(o) is before it's head, e.g.:
m1: skip "abcde" -1
m2: skip "123" -2
;) .abcde
;) +
;) ..123
;) =
;) .a123e
;) ^ a remains because it's "undefined" in m₂-th buffer (before the head)
;) ^ e remains because it was after m₂-th tail
This brings sort of symmetry: items before the head and items after the tail are applied from m₂ to m₁ using the same rules.
And so on...
These can be expressed through other high level functions, without access to (Bₖₜ(i),Nₖₜ,Kₘₜ,Oₘₜ) state.
(back m) = (skip m -1)
(next m) = (skip m 1)
(at m j) =
(skip m j-1), if j > 0
(skip m j), if j ≤ 0
at can be constrained: j ≠ 0 (an error otherwise)
(offset? m1 m2) = (index? m2) - (index? m1)
(length? m) =
0, if (index? m) ≥ (index? tail m)
(index? tail m) - (index? m)
(tail? m) =
yes, if (index? m) ≥ (index? tail m)
no
(head? m) =
yes, if (index? m) ≤ (index? head m)
no
Alternatively head? and tail? can check for index equality only.
(empty? m) =
yes, if (length? m) = 0
no
(single? m) =
(last? m) =
yes, if (length? m) = 1
no
(first m) = (pick m 1)
(second m) = (pick m 2)
(third m) = (pick m 3)
(fourth m) = (pick m 4)
(fifth m) = (pick m 5)
(last m) =
none, if (empty? m) = yes
(pick tail m -1)
Note: this (and high-level definitions) is all wishful thinking right now and very few of these invariants/definitions hold in the current build.
An idea is to allow series' offset (index?) take any integer value.
R2 could internally work with pre-head and past-tail offsets but it was inconsistent about it:
>> index? #(block! [a] -2) ;) can construct a pre-head block
== -2 ;) `index?` doesn't lie that offset is negative
>> index? b: #(block! [a] 10)
== 2
>> append b [1 2 3]
== [a 1 2 3]
>> index? b
== 2 ;) so the constructed block was not past-tail
>> b: tail "1234567890"
== ""
>> clear head b ;) an R2 way to construct a past-tail block
== ""
>> index? b
== 11 ;) works! and somehow it's not = 2! OMG!
>> c: b repeat i 9 [append b i probe index? c]
2 ;) observe:
3 ;) I'm adding items to `b`
4 ;) but it's `index? c` that changes every time
5 ;) and initially it changed from 11 to 2 !!
6
7
8
9
10
== 10
In Red this is a different mess:
- no way to construct a pre-head block (except via R/S - but that will crash it for certain)
- when offset is past-tail,
index? cdoesn't lie about it - it will always report 11 in the previous snippet - various functions deal with past-tail differently: https://gitter.im/red/red?at=5da8508ef88b526fb95455ef ,
index? skip m 1(positive skip) can be less thanindex? m, which is confusing.
But what if we didn't have any offset restriction? E.g. if m is at head, skip m -1 would go ahead of it, and index? m would be -1, and so on. We would have:
- a lot simpler invariants (see the next section), that would not depend on data, and
- more versatility in series modifications, though we'll have to define SRFs behavior with negative offsets (see
changedefinition above)
This may also ease our life if we will ever make a slice! datatype (kinda like series, but with controlled tail, not bound to the data size). If we will though, all /part refinements will become obsolete as we will be able to construct slices of m on the fly with part m function or something.
Please speak your mind in the discussion REP.
(index? skip m j) = j + (index? m) ;) requires free index
(back next m) = (next back m) = (m) ;) requires free index
(skip skip m j -j) = (m) ;) requires free index
(index? head m) = 1
(index? tail m) ≥ (index? head m) ;) tail cannot precede head
(index? tail m) = (1 + length? head m)
(length? m) ≥ 0
(index? m) = (clear head m index? m) ;) index? is not affected by tail
For functions supporting series & integer part (this especially affects find & select):
(func m1 /part m2) =
(func m2 /part m1) =
(func m1 /part offset? m1 m2) =
(func m2 /part offset? m2 m1)
For functions supporting only integer part (mold, form, read, write):
(func m1 /part j) = (func m1 /part 0) if j < 0
Or alternatively negative /part for these can be an error.
(func ... /into m) = (append m func ...) ;) see #4109
(repend m x) = (append m reduce x)
Will this ever work for reduce/compose/repend when m contains code that modifies m?
(select m x) = (first find/tail m x), when m is a series (x can be too)
When m1 and m2 are series (even if of the same buffer):
(change m1 m2) = (m3: copy m2 remove m1 /part length? m2 insert m1 m3)
(change m1 m2 /part p) = (m3: copy m2 remove m1 /part p insert m1 m3)
See https://github.com/red/red/issues/4099 about this one:
(change m1 m2) = (change m1 copy m2)
Some find refinements:
(find/reverse m x) = (find/last m x /part head m)
(find/last m x) = (find/reverse tail m x /part m)
(find/tail m x) =
(skip find m x length? x), if x is a series
(next find m x) otherwise
(find/match m x) =
(find/tail m x /part length? x), if x is a series and no /only
(find/tail m x /part 1) otherwise
And so on...
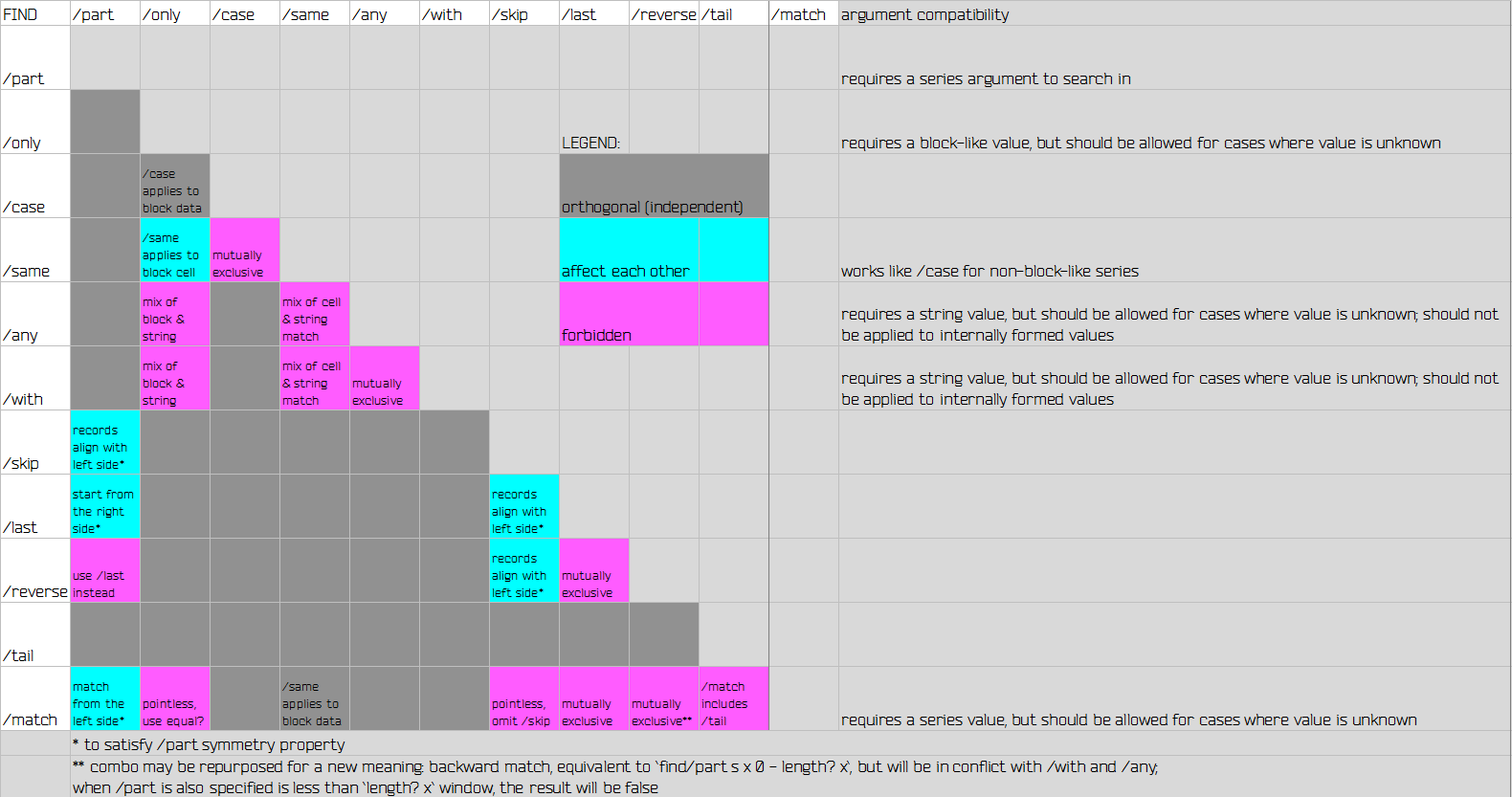
Here's one for find (notorious for being refinement-overloaded)
General principles:
- Define what refinements affect or conflict with one another
- Define if refinements expect narrower argument space, decide if it should be ignored or enforced (with an error), document it briefly
- Each cell, when it's not immediately obvious, should contain enough hints to replicate the reasoning behind it
Both Red and Red/System are published under the BSD license. The runtime is published under the BSL license.